It is often useful to remove the units from an equation. We can see which physical mechanisms are more important and the equation to be solved is simpler. We scale all variables so that the variables become dimensionless. We can solve the equation relative to properties of the system e.g. the period.
To make an equation dimensionless one must do the following:
-
Identify all the independent and dependent variables, e.g.
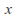having dimension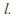
-
Replace each of them with a quantity scaled relative to a characteristic unit e.g.
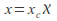where
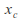is constant and has dimension
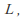and
is variable and dimensionless;. -
Rewrite the system of equations in terms of their new dimensionless quantities.
-
Divide through by the coefficient of the highest order derivative term;.
-
Choose the scale factors so that as many terms as possible have coefficient 1.
Example: Make
dimensionless.
1. The independent variable is
and the dependent variable is
2. Let
and
whereand
are constants to be defined later.
3. Since
we have
4. The coefficient of the highest order term is
and dividing by this leads to
5. Choose
and
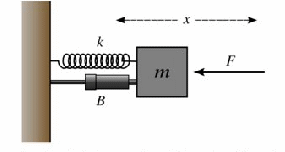
Example: Make
dimensionless where
is the equilibrium position.
This is the equation of the system below.
1. The independent variable isand the dependent variable is
-
Make
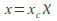and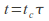
then follow the procedure in 3 above to get -
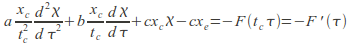
Divide through by the leading coefficient
to give
5. Choose
and add 1 to both sides to give
where