Poisson's Equation

We often need to find the potential at each point in a region of space due to a distribution of charges. We start at Gauss's Law(1)

The electric field is given in terms of the potentialbyand we can substitute this into (1) to obtain(2)

The combination div grad is known as the Laplacian operator and writtenIt is a second order differential operator. In Cartesian coordinates it takes the formand substituting this into (2) gives

This equation is known as Poisson's equation.

The problem of finding the potential of a distribution of charges is now reduced to finding the solution to a second order differential equation. Many distributions involve some sort of symmetry or uniformity.

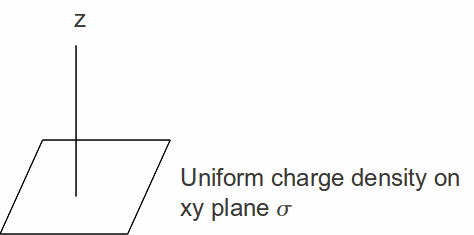
Charge may be distributed uniformly on a plate and we need to find the potential at a distance from the plate. There is symmetry in the xy plane.

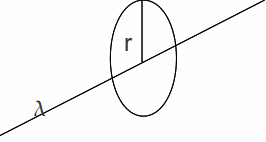
or on a thin long wire and we need to find the potential at a radial distance r. There is radial symmetry.

Obviously a point charge or chage distribution on the surface of a sphere have spherical symmetry. By using appropriate coordinater systems for each case of symmmetry, the Poisson equation can be quickly solved.