\[\beta\]
per unit length.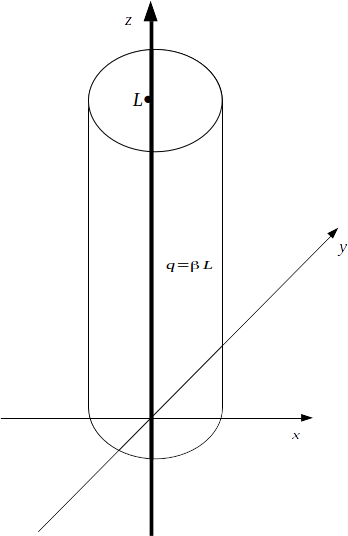
\[S\]
enclosing a charge \[q\]
, Gauss's Law gives \[\int_S \mathbf{E} \cdot \mathbf{n} dS = \frac{q}{\epsilon_0} \]
The cylinder drawn has three surfaces. For surfacesat the ends of the cylinder the electric field, which is radial, is perpendicular to the normal, which is along the wire, so
\[\int_{S_{TOP}} \mathbf{E} \cdot \mathbf{n} dS = \int_{S_{BOTTOM}} \mathbf{E} \cdot \mathbf{n} dS =0 \]
and only the curved surface of the cylinder contributues to the integral.For the curved surface
\[\mathbf{E}\]
is radially out by symmetry and the normal is also radially out. Hence, using cylindrical polar coordinates,\[\begin{equation} \begin{aligned} \int_S \mathbf{E} \cdot \mathbf{n} dS &= \int^L_0 \int^{2 \pi}_0 E r d \theta dz \\ &= 2 \pi r L E \end{aligned} \end{equation}\]
Hence
\[2 \pi r LE = \frac{L \beta}{\epsilon_0} \rightarrow \mathbf{E} = \frac{\beta}{2 \pi r} \mathbf{e_r}\]
