Applications of the Chain Rule 2

When the volume of a solid is increasing, so in general are the dimensions and surface area of the solid. If the solid maintans it shape, so that at each point in time it has a mathematically similar shape to the original, then we can use the chain rule to relate the rate of increase of volum to the rate of increase of the surface are or length of the solid.

Suppose that a cube is increasing in volume at the rate of 4 cm ³ /s. The cube has sides of lengthso the volume of the cube isand the surface area isSuppose it is desired to find the rate at which the surface area is increasing when

We can use the Chain Rule, which states

and

From the first of these, withso that whenthen

cm/s

From the second of these, withso that when

cm ² /s.

Alternatively, we could have used the Chain Rule in the form

With

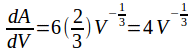
Whensoand

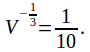
cm ² /s.