We can use the binomial theorem to expand and simplify expressionsof the form![]() where
where![]() isany positive whole number.
isany positive whole number.
The general expansions is
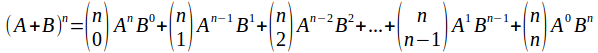
Example:
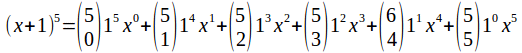
The coefficients gere have a special signifucance.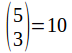 isthe number of ways in which a term with
isthe number of ways in which a term with ![]() canbe generated when
canbe generated when![]() isexpanded fully.
isexpanded fully.
Suppose we have 5 men of which three are to be selected forpromotion. The number of ways in which three men can be selected fromthe five is the same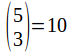 generatedby the binomial expansion above. When choosing a selection of
generatedby the binomial expansion above. When choosing a selection of![]() froma possible
froma possible![]() wesay '
wesay '![]() choose
choose![]() 'We may write it as
'We may write it as![]() or
or![]()
Given a set of![]() individuals,the total number of selections of any size that can be made is
individuals,the total number of selections of any size that can be made is![]() Thiscan also be deduced from the binomial theorem.
Thiscan also be deduced from the binomial theorem.
The total number of selections of size 0 is![]()
The total number of selections of size 1 is![]()
The total number of selections of size 2 is![]()
![]()
![]()
![]()
The total number of selections of size![]() is
is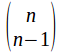
The total number of selections of size n is![]()
Adding all these up gives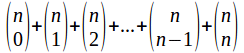 andwe can write this as
andwe can write this as![]()
