Notation

Functions are labelled by letters – generallythough in fact any may be used, Greek letters too. Each function has an associated argument. The function is defined by what it does to the argument.

The argument ofisthe argument ofisand the argument ofisNot that it is not the action of the function onthat defines the function, but the action of the function on the argument.

IfthenandWe can label all of these byand it is understood thatsquares whatever is put into it. The graph oftherefore is only well understood when the argument isand we can associate with the functiona set of pointsIf the argument changes, the graph ofwill change if the– axis remains the– axis, but we can change the labelling of the– axis in the same way to preserve the shape of the graph. Suppose that we change the argument offromtoKeeping the-axis unchanged would have the effect of moving the graph 4 to the right, but if we changing the labelling of the– axis fromtothis is not necessary. This is shown below for the function

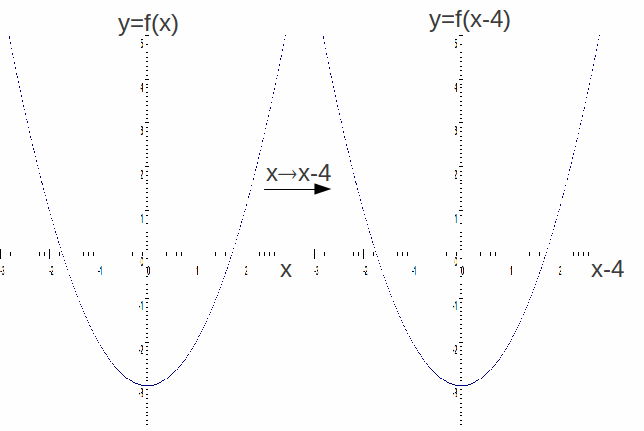
Note that the functionsquares the argument and subtracts 3, so