If a function is one to one, so that every value in the domain is associated with a unique value in the codomain and every value in the codomain is associated with a unique value in the domain, then the function can be inverted.
An invertible function can have no turning points (minima or maxima). The gradient must always have the same sign, and if it is zero, can only be zero at a single point on any interval. That is, the function must be always either increasing or decreasing.
and
are invertible function. In fact they are inverses of each other so that
and
The graphs of
and
are shown below. Each is the reflection of the other in the line
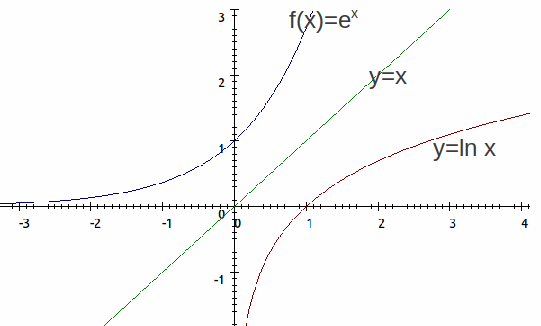
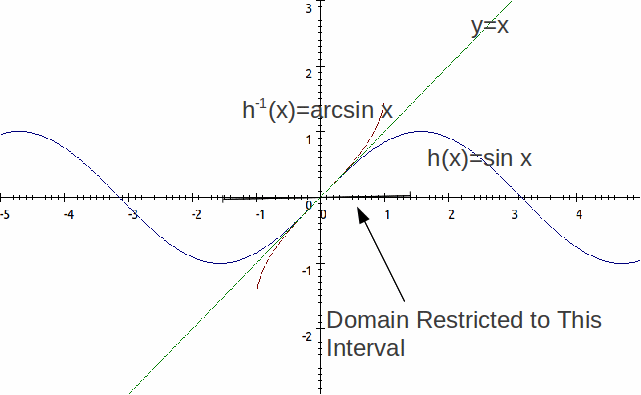
We can often make a non – invertible function invertible by restricting the domain. For example,
is non invertible because it is not one to one:
for all
We can however, make it invertible by restricting the domain to
so that the function is one to one on that domain, then it will be invertible with that restriction.
There is a procedure for finding the inverse of a one to one function
-
Make
the subject. -
Interchange
and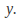
-
Replace
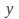with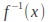
For example, if
then applying step 1 gives
Now apply step 2 to get
And finally step 3 to get