\[y=A+B^{kx}\]
.Each pf
\[A, \: B, \: k\]
can be positive or negative and the sign and magnitude of each determines the shape of the graph.The graph has an asymptote in the line
\[y=A\]
. If \[B \gt 0\]
, the graph lies above the asymptote. If \[B \lt 0\]
the graph is below the asymptote.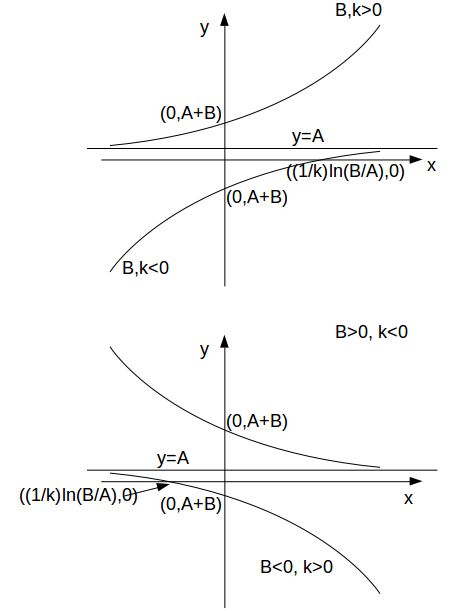
\[y\]
- axis is at \[(0,A+B)\]
.There is no
\[x\]
- intercept if \[A=0\]
or if \[A, \: B\]
have the same sign. If \[A, \: B\]
have opposite signs then the \[x\]
intercept is at \[(\frac{1}{k} ln(\frac{B}{A}),0)\]
. 