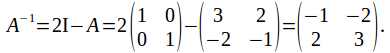If we have a matrix
that satisfies the equation
where
is the identity matrix then we can find
by multiplying throughout by
so the above equation becomes
and
o
We can rearrange this to makethe subject.
The process is a lot like ordinary algebra, with the exception that when using matrices we must be careul to multiply byon the left throughout or on the right throughour, since matrix multiplication is not commutative. This does not matter if onlyand the identity matrix appear in the equation, but it is still a good habit to acquire.
Example: If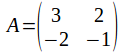
then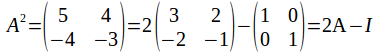
so that multiplying throughout bygives
and