Multiplying to Get Zero

If two numbers are multiplied to get zero then at least one of the numbers has to be zero. Concisely,

ifthenoror bothand

This is not true for matrices. It is possible to multiply non – zero matrices together to obtain the zero matrix.

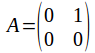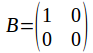For example, ifandthen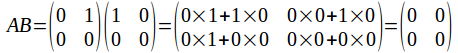

When squaring a number, or raising a number to a power, the result is zero if, and only if, the number is zero. Concisely, if x^n =0 for n=1,2,... then x=0. Again, this is not true for matrices. If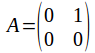then

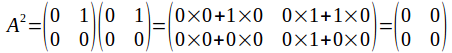
Matrices can be through of as a more general type of number than the real numbers. It is possible that things multiply to give zero.