Cryptography hiding and uncovering information in codes. Whenever information is required to be sent from one place to another so that even if it were intercepted it would still be secure, it must first be put in the form of some code. When it is received by its intended recipient, it must then be decoded.
Originally it was used to encode written messages. Both sender and recipient would have codebooks which they would use to code and decode the message. Today, it is used in computer networks to keep them secure, and to make sure that emails, banking data, government communications, telephone calls, internet traffic, cannot be easily intercepted and decoded to extract information.
Messages are sent in code or cipher form. The method of converting text to cipher text is called enciphering and the reverse process is called deciphering. Codes can be created with matrices, using simple matrix addition and multiplication. The result is written as a list of numbers and the reverse process is applied at the receiving end to read the message.
A simple code may be constructed by giving each letter a number.
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
0 |
The word 'WIRE' would then be encoded as 23 9 18 5. We could write this in matrix form as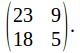
A matrix could then be added, mod 26, to this matrix to give another layer of security. Suppose we add the matrix
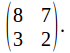The matrix to be transmitted is then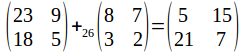
The message 'WIRE MONEY QUICK' could be broken into groups of four letters and
each group encoded.
(WIRE)(MONE)(YQUI)(CKKK)
Note that the last letter is repeated to make a group of four letters.
The matrix representing 'MONE' is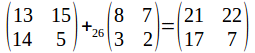
The matrix representing 'YQUI' is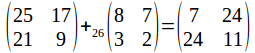
The matrix representing 'CKKK' is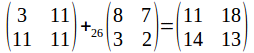
The message to tne sent is 5 15 21 7 21 22 17 7 7 24 24 11 11 18 14 13.
The additive inverse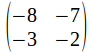
is required to decode the message.