Often a physical situation can lead to an equation invoving a polynomial for which we have to find the roots. One of the roots of the equation will be the solution of the polnomial. If the polynomial is of higher degree than a quadratic, it may only be possible to find the solution numerically, possibly using a graphic package.
The diagram below shows a ladder leaning against a wall. The ladder is 10m long and rests against a 1 m 3 box. The ladder reaches x m up the wall. Find
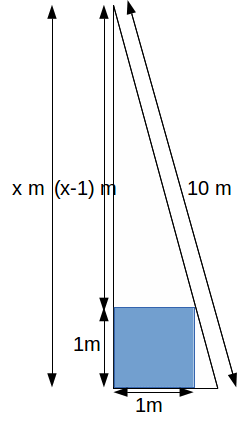
We can extract similar triangles from the above diagram and use the ratios of their lengths to derive a polynomial equation in
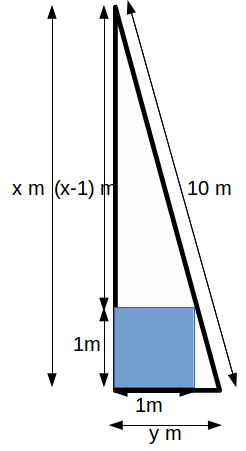
From the diagram above, using Pythagoras theorem to find
gives 
so base divided by height gives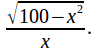
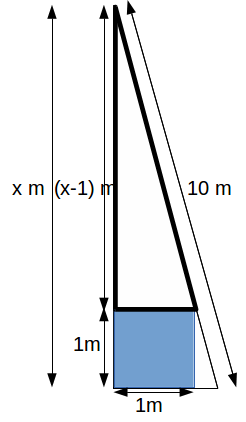
From the diagram above base divided by height gives
These two ratios must be the same since the triangles are similar so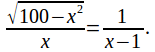
Rearrangement of this expression gives
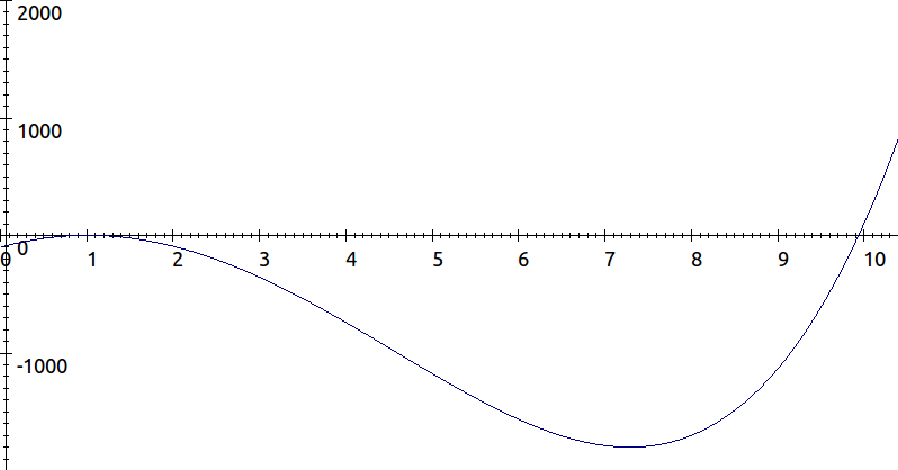
The graph of
is shown below. The required root is obviously at
The root can be found using a graphical calculator.
