Turning Points of a Polynomial

Some quadratic expressions do not have roots. That is, ifthere may be no value offor which f(x)=0. On the otrher hand, every quadratic has a turning point. This is a simple consequence of the fact that the value ofthat defines the turning point is the solution toor 2ax+b=0 The x value of the turning point is then

The turning point may be either a maximum or a minimum, depending on the value of

Ifthe turning point is a minimum.

Ifthe turning point is a maximum.

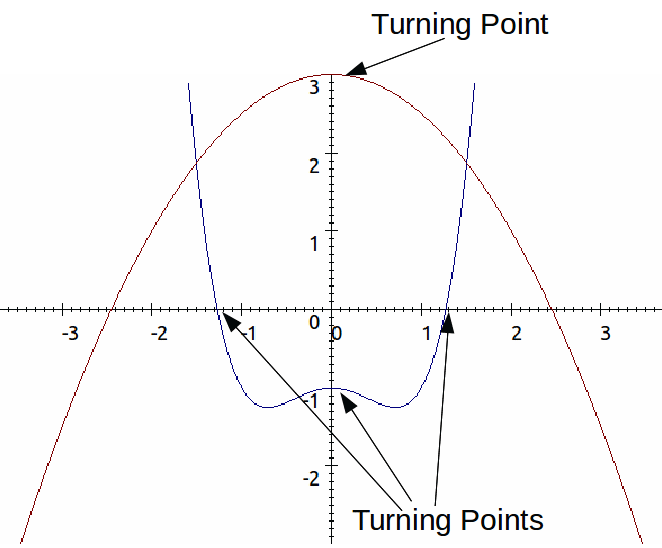
We can generalise this to higher order polynomials.

Ifis a polynomial of even degree equal toand the coefficient ofis positive, then the polynomial has at least one turning point and a least one minimum. If the polynomial has only one turning point then that turning point is a minimum. If the coefficient of x^n is negative then the polynomail has at lest one turning point and at least one maximum. If the polynomial has only one turning point then that turning point is a maximum.

For polynomials of odd degree, there is no guarantee of the polynomial having a turning point. To give the simplest ecamplyhas a stationary point atbut it is not a trning point becauseexcept atsois increasing.

For polynomials of both even and odd degree, we can say this: if the polynomial has roots, then between every two roots – crossings of the x axis - , there is at least one turning point. Possible cases are shown below.