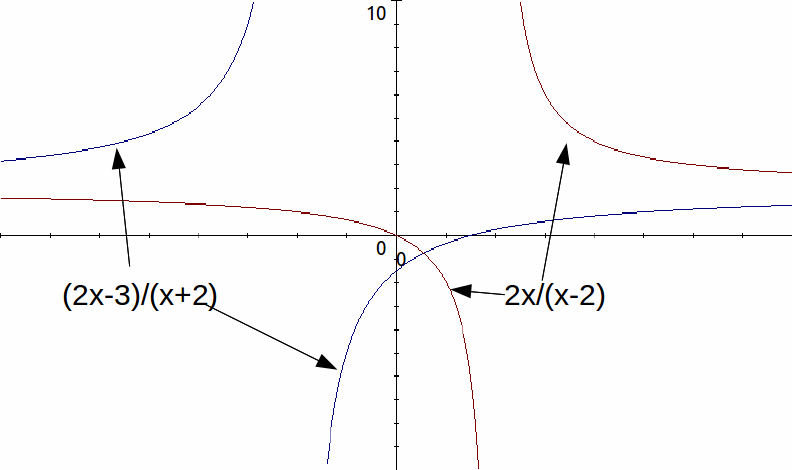
To solve an inequality of the form
moving everyhing over to one side, simplify and analyse sign changes for each factor in numerator and denominator.
For this example, moving eveything to the left hand side gives
Simplifying by adding as fractions gives
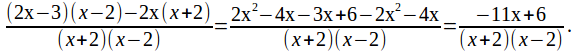
Changes of sign for each factor are summarised in the following diagram, and for the whole expression- the bottom line, labelled
).
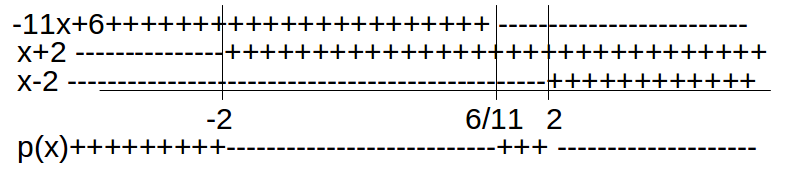
for
and x>2. This is illustrated for original question in the diagram below.
