Proving trigonometric identities using induction follows the usual route. The identity usually involves summing a trigonometric series or simplifying a product.
1. Define the identity to be proved so that the statement is equivalent to '
is true'.
2. Prove the identity for
or
to show that the statement
or
is true.
3. Assuming the statementis true, prove the statement
Example: Use induction to prove the identity
Ifthe identity becomes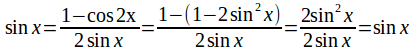
sois true.
Suppose then thatis true so that
(1)
is the statement that
Adding
to both sides of (1) gives
Concentrate on the left hand side.
(2)
Use
with
and
to obtain
(2) becomes
so P(k+1) is proved.