Quadratic exquations, including equations of circles, ellipses,hyperbolas and the familiar parabolic equations y=ax^2 +bx +c, arisenaturally as a result of considering the intersection of a plane witha cone.
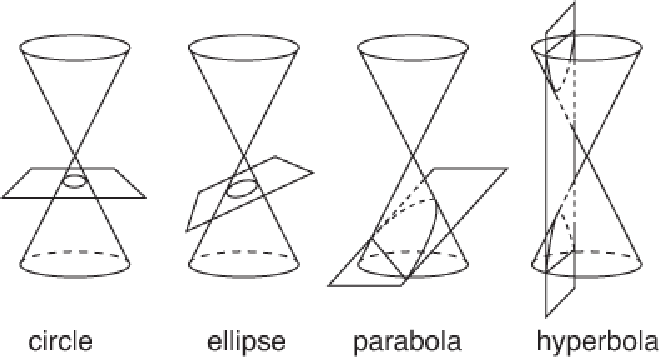
Starting with a horizontal plane the intersction describes acircle with equation![]()
Tilting the plane with respect to the cone deforms the circle intoan ellipse with equation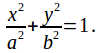
Tilting it still further so that the plane is parallel to aslanted side of the cone means that the ellipse never closes at thelower end, andf it becomes a parabola with equation![]()
Ttilting the plane further to the vertical so that it passesthrough the vertex where the upper and lower cones meet divides theintersection into two parts, with one each intersecting the upper andlower halves. The curve is now a hyperbola with equation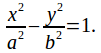
The constants for each equation are not connected in general.
