100m of fence is used to enclose part of a field in the shape of a rectangle. One side of the enclosure is formed by a hedge.
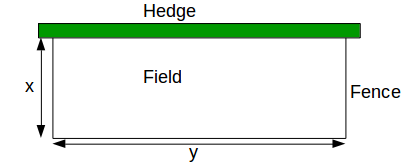
\[x\]
and \[y\]
then the area is \[A=xy\]
and since there is 100m of fencing, \[100=2x+y\]
.The second equation can be arranged to give
\[y=100-2x\]
. In terms of \[x\]
the area is \[A=x(100-2x)=100x-2x^2\]
.We can find the maximum of this expression by completing the square.
\[\begin{equation} \begin{aligned} A &= 100x-2x^2 \\ &= -2(x^2-50x) \\ &= -2((x-25)^2-25^2) \\ &= -2 \times -(25)^2-2(x-25)^2 \\ &= 1250-2(x-25)^2 \end{aligned} \end{equation}\]
The maximum area is
\[1250m^2\]
, occurring when \[x=25m\]
. 