The solutions of a quadratic equation
are given by
In order for the equation to have real solutions, we must have that
since we cannot take the square root of a negative number to obtain a real number. This means that if
the equation has no real solutions. If
there are solutions, given by
Obviously these two solutions are the same
If b^2 -4ac >0 then the solutions are distinct, given by
and
The expression
is called the discriminant and the number of solutions of a quadratic is determined solely by whether it is positive, negative, or zero. It is often labelled
The number of roots, and their significance on the graph of the quadratic, is illustrated in the graph below.
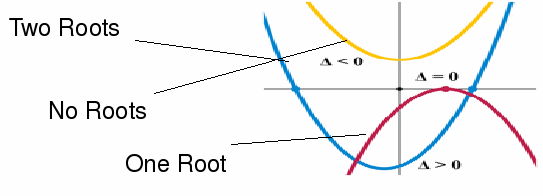
Notice that if there are no roots, the graph doesn't cross the x – axis at all.
If there is one root, the graph touches the x – axis (at one point) but doesn't cross it.
If there are two roots, the graph crosses the x – axis in two separate places.
Suppose that
the discriminant is
so the equation has no solutions.