The Bisection Method

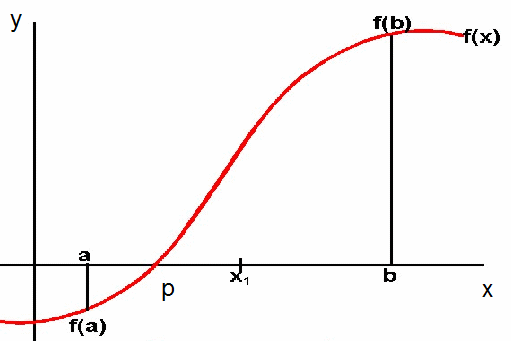
Supposeisa continuous function on some intervalwithandof opposite sign. By the intermediate value theorem, there issuchthatFor simplicity, let's assume there exists only one root inas shown.

Bisection gives a simple and robust method for bracketing the rootThe algorithm works as follows:

Take the midpointas a first guess and calculateIfandare

of opposite sign then the root lies in the interval(Conversely,ifhas the opposite

sign tothen the root lies in the interval)

This procedure can be repeated iteratively, e.g. taking a second guessfrom

the example above.

At each iteration we halve the size of the intervalthat contains the rootand after n

iterations of the procedure we have reduced the uncertainty indown to,

Example: The functionhas a root in the intervalsinceandThe actual root is of course

In the table,andis the exact absolute error.

Advantages of the method

i. provided the function is continuous on an intervalwithbisection is

guaranteed to work.

ii. the number of iterations needed to achieve a specific accuracy is known in advance.

Disadvantages of the method :

i. the method is slow to converge.

ii. the errors inand indo not necessarily decrease between iterations. Note that,

in the example aboveis closer to(andcloser to 0) than the next 3 iterates.

Also, no advantage is taken of intermediate good approximations.