There is only so much to go around, even more so now with the Earth's resources running low and the price of everything. We have to make the most of what we have, and decide what things should be used for so that the most use can be got out of them.. W will consider the very simplest type of problem – how to enclose the most area for a fixed length of fencing. Suppose then that we have 100m of fencing. The fencing is to enclose a rectangle shaped field, but one side of the field will be made up of a hedge so we will not need to use the fencing for this side.
From the diagram above the area of fencing is
and we have to find the maximum area and the value of
that gives this maximum.
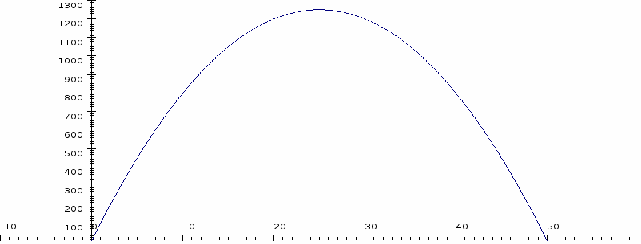
The graph ofagainst Area is shown above. The maximum Area seems to be
and the value ofis 25. We could have solved this problem by completing the square:
so
when
or by differentiating to find the turning point of
