Projectiles

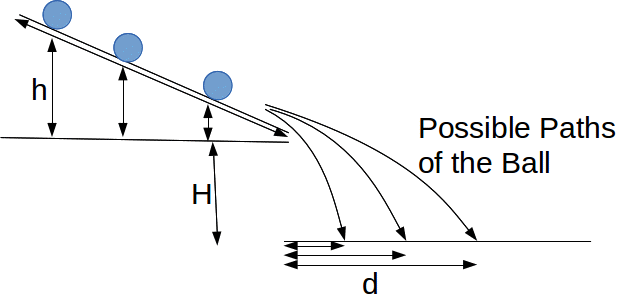
Over 400 years ago, the Italian scientist Galileo attempted to find a mathematical description of the motion of projectiles. One of his experiments consisted of rolling a ball down a grooved ramp placed at a fixed height above the floor and inclined at a fixed angle to the horizontal. The ball left the end of the ramp and descended to the floor.

We can apply conservation of energy to the motion of the ball down the ramp. The ball loses an amount of gravitational potentia; energy equal toso must gain an equal amount of kinetic energy,We can write

If the ramp is inclined at an angleto the horizontal, the horizontal speed of the ball at the end of the ramp isand this will be constant since when the ball leaves the ramp there will be no horizoontal forces acting on the ball – gravity is a vertical force.If the time for the ball to hit the floor after it leaves the ramp is t, then(1)

For a particle subject to an accelerationwith initial velocitymoving a distancein a timeApplying this to the vertical motion of the ball after it leaves the ramp (remember that and) so thatRearranging (1) givesso that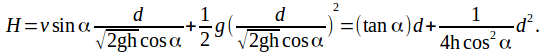

The last expression is a quadratic equation insinceandare constant.