Lines are parallel if they have the same direction vector, or if the direction vector of one line is a multiple of the direction vector of another line. It is possible however for two lines to have the same direction vector, or have one direction vector a multiple of another, but different starting points, but still be the same line.
Consider the two lines
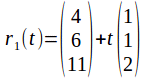and
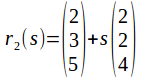
These two lines are parallel since the direction vector of the second is twice the first. The lines also pass though a common point, since by putting corresponding – x, y and z - components equal, we obtain the equations
These can be solved to obtain solutions for
and
satisfying all three equations:
and
Since the lines have the same direction vector and have pass through a common point, they are the same line.
The lines below are not the same.
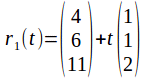and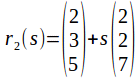
These lines do not have direction vectors that are multiples of each other so cannot be the same line.
The lines below are not the same.
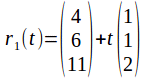and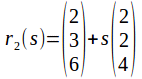
The lines are the same as in the first example, with the exception that the start point of
is different. The equations to solve become
The solutions to the first two areand
but these do not satisfy the third equation so the lines cannot be the same.