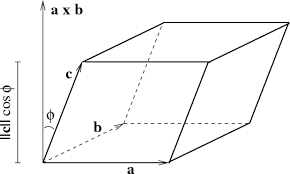
\[\vec{a}, \: \vec{b}, \: \vec{c}\]
the area of the base - formed by vectors \[\vec{a}, \: \vec{b}\]
is the magnitude of the vector or cross product of \[\vec{a}\]
and \[\vec{b}\]
.\[Area \: of \: Base = \| \vec{a} \times \vec{b} \|\]
(
\[\vec{a} \times \vec{b}\]
is a vector perpendicular to both \[\vec{a}\]
and \[\vec{b}\]
).If the third vector defining the parallelepiped is
\[\vec{c}\]
then the volume of the parallelepiped is given by the the area of the base times the projection of \[\vec{c}\]
onto the vector \[\vec{a} \times \vec{b}\]
\[Volume=\| \vec{a} \times \vec{b} \| \vec{c} \cdot ( \frac{\vec{a} \times \vec{b}}{\| \vec{a} \times \vec{b} \|} )=(\vec{a} \times \vec{b}) \cdot \vec{c}=\left| \begin{array}{ccc} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right|\]
