The Composite Simpon's Rule

We need to find a numerical estimate for

Considerintervalsof widthwith equispaced points

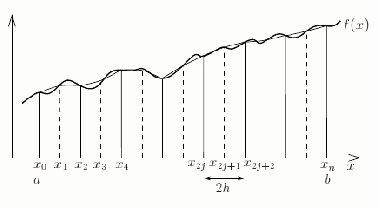
There existssuch that

Using, we can rewrite the composite Simpson's rule as

So, the composite Simpson's rule is 4th order accurate.

For example ifon the intervalwith 10 intervals sowe can estimate an upper bound for the error for