The center of a group![]() written
written![]() is the set of elements
is the set of elements![]() that satisfy
that satisfy![]() for all
for all![]() – that this, they commute with all
– that this, they commute with all![]()
The center is a subgroup of![]() and is abelian, since every element of
and is abelian, since every element of![]() commutes with every element of
commutes with every element of![]() so also commutes with every element of
so also commutes with every element of![]() We can prove that
We can prove that![]() is a subgroup of
is a subgroup of![]() using the subgroup axioms.
using the subgroup axioms.
S1:![]() imply
imply![]() If
If![]() then
then![]() and
and![]() for all
for all![]()
![]() so
so![]()
S2:![]()
![]() for all
for all![]() so
so![]()
S3:![]() implies
implies![]()
![]() implies
implies![]() for all
for all![]() so
so![]()
As a subgroup,![]() is normal since
is normal since![]() for all
for all![]() so
so![]() and
and ![]() The quotient group
The quotient group![]() is well defined.
is well defined.
A group![]() is abelian if and only if
is abelian if and only if![]() At the other extreme, a group is said to be centerless if
At the other extreme, a group is said to be centerless if![]()
Consider the map![]()
This is a group homomorphism, and its kernel is precisely![]() since
since![]() if
if![]() Its image is called the inner automorphism group of
Its image is called the inner automorphism group of![]() denoted
denoted![]()
Examples
-
The center of a nonabelian simple group is trivial, since simple groups have no nontrivial normal subgroups.
-
The center of the dihedral group
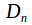 is trivial when
is trivial when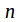 is odd. When
is odd. When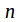 is even, the center consists of the identity element together with the half rotation.
is even, the center consists of the identity element together with the half rotation. -
The center of the quaternion group
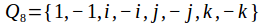 is
is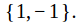
-
The center of the symmetric group
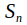 is trivial for
is trivial for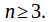
-
The center of the alternating group
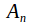 is trivial for
is trivial for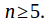
-
The center of the general linear group
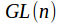 is the collection of scalar matrices
is the collection of scalar matrices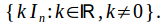
-
The center of the orthogonal group
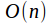 is
is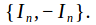
-
The center of the multiplicative group of non-zero quaternions is the multiplicative group of non-zero real numbers.
-
Using the class equation one can prove that the center of any non-trivial finite p-group is non-trivial.
-
If the quotient group G / Z(G) is cyclic, G is abelian.
