Onto or Surjective Functions

Suppose we have two setsandWe can define a function acting on the elements ofwhich sends those elements ofonto unique – needed so that f is a function, since a function cannot be one to many - elements ofIf it is the case that for every elementofthere exists somein such thatthenis said to be a function fromontoIn this caseis said to be a surjective function or surjection.

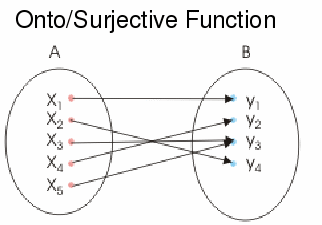
Note thatdoes not need to be one to one to be surjective. We could takeandfor allthenis onto

The above functions are discrete, but we can define function that act on intervals.

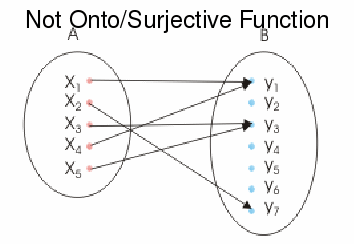
is not ontobecause there is nofor which

If instead we defineas

thenis onto. We can always make a function onto some subset ofin this way because by definition, a function is onto it's image.