Solving Differential Equations Using Separation of Variables

The separation of variables method is a technique for solving partial differential equations subject to boundary conditions and is used to solve problems where

1. The partial differential equation to be solved is linear and homogeneous.

2. The boundary conditions are of the form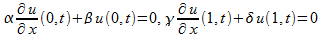where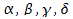are constants.

3. The solution obeys the initial condition

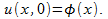
I will illustrate the method with an example.

(1)

We look for solutions of the form

Substitution into the original differential equation givesDivide byto givesThe left hand side is a function of t only and the right hand side is a function of x only. Since x and t are independent variables, we must have that both sides are constant. Suppose that both sides equal k. We can write

andor(2)

Ifthe solution to the first isThis solution tends to infinity astends to infinity so we must havePutthen the two equations (2) becomewith solutionsso all solutions take the formsinceare arbitrary. We now fit these solutions to the boundary conditions.

Since the original equation is linear, any linear combination of these solutions is also a solution. We can write the most general solution to (1) as

We now fit these solutions to the initial condition

In general fitting the most general solutionto the initial condition will involve finding the coefficients of a Fourier series.