The Laplace transformation can be used to solve differential equations. Applying the Laplace transformation transforms differential equations into algebraic equations. We can solve the algebraic equation and apply the inverse transform from a table of Laplace transforms to obtain the solution to the original differential equation.
The transformation requires the formulae
![]() and
and![]()
Example: Solve the differential equation![]() with
with![]()
Applying the Laplace transformation gives![]()
![]()
![]()
Example: Solve the differential equation![]() with
with![]()
Applying the Laplace transformation gives![]()
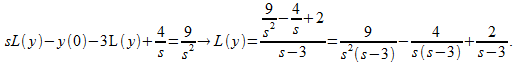
![]()
Example: Solve the differential equation![]() with
with![]() at
at![]()
The transformed equation is![]()
![]()
Solve the differential equation![]() with
with![]() and
and![]()
The transformed equation is![]()
Hence![]()
Applying the inverse transformation to each term gives![]()
