\[2x+y+z=4\]
. What is the volume of the tetrahedron?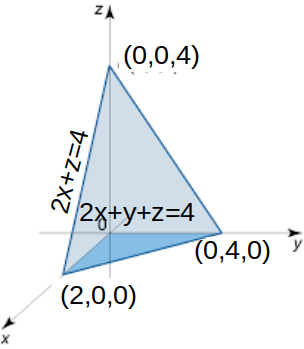
\[dx\]
, length \[y\]
and height \[z\]
. The volume of the element is \[dV=ydxdz=(4-2x-z)dxdz\]
.We can take the limits of
\[x\]
and \[y\]
as \[, \; 2- \frac{z}{2}\]
and \[0, \l 4\]
respectively. The volume is\[\begin{equation} \begin{aligned} V &= \int^4_0 \int^{2- \frac{z}{2}}_0 (4-2x-z)dxdz \\ &= \int^4_0 [ \int^{2- \frac{z}{2}}_0 (4-2x-z)dx ] dz \\ &= \int^4_0 [4x- x^2-xz]^{2- \frac{z}{2}}_0 dz \\ &= \int^4_0 4-2z+ \frac{z^2}{4} dz \\ &= [ 4z- z^2 + \frac{z^3}{6} ]^4_0 = \frac{32}{3}\end{aligned} \end{equation}\]
