Th Voltage Law: The voltage around a loop in the circuit add up to zero.
The Current Law: The sum of currents into any junction in a circuit adds up to zero.
Consider the circuit below.
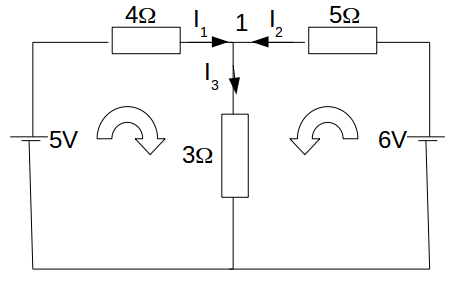
\[I_3-I_1-I_2=0 \rightarrow I_1+I_2-I_3=0\]
Applying the voltage law to the left hand loop, and
\[V=IR\]
to each resistor gives
\[5-4_I-3I_3=0 \rightarrow 4I_1+3I_3=5\]
.Applying the voltage law to the right hand loop, and
\[V=IR\]
to each resistor gives
\[3I_3+5I_2-6=0 \rightarrow 5I_2+3I_3=6\]
.We have three simultaneous equations.
\[I_1+I_2-I_3=0\]
\[4I_1+3I_3=5\]
\[5I_2+3I_3=6\]
We can write this in matrix form as
\[ \left( \begin{array}{ccc} 1 & 1 & -1 \\ 4 & 0 & 3 \\ 0 & 5 & 3 \end{array} \right) \begin{pmatrix}I_1 \\ I_2 \\ I_3 \end{pmatrix}= \begin{pmatrix}0\\5\\6\end{pmatrix}\]
Hence
\[ \begin{pmatrix}I_1\\I_2\\I_3\end{pmatrix}={\left( \begin{array}{ccc} 1 & 1 & -1 \\ 4 & 0 & 3 \\ 0 & 5 & 3 \end{array} \right)}^{-1} \begin{pmatrix}0\\5\\6\end{pmatrix}= \begin{pmatrix} {22/47} \\ {27/47} \\ {49/47} \end{pmatrix} \]
