Open Sets and Continuity in a Metric Space

Theorem

Supposeis a map from a metric spaceto a metric space

The statements 'is continuous'

and

'for all open setsis open in

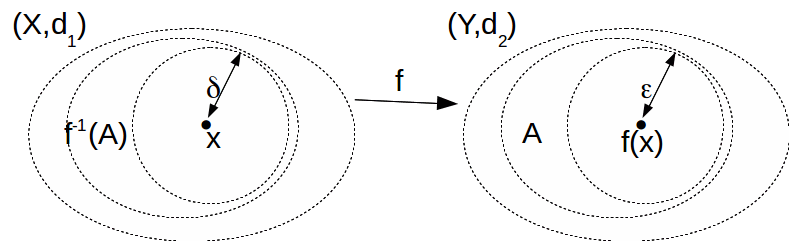
Proof

Supposeis continuous andis an open subset ofLetthen

Sinceis open there existssuch that

Sinceis continuous there existssuch that

Hence (1)

Forexists such that (1) is true henceis open in

Conversely suppose thatis an open subset ofthenis an open subset ofIf then there existsis an open subset ofHenceis an open subset ofThen there existssuch thator