Possible Metrics

Three basic metrics are illustrated below in ordinary two dimensional Euclidean space. Each metric illustrates the the locus described by

For

For

For

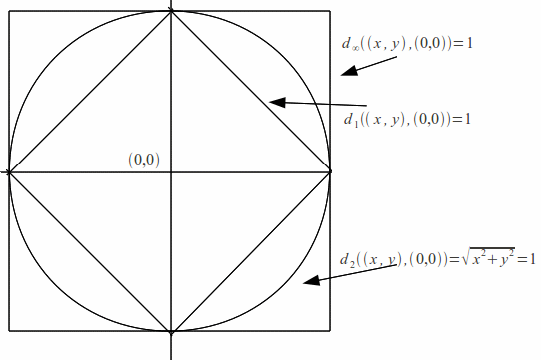
All of the metrics above are topologically equivalent. They all give rise to the same metric space, with the same open sets.. This is easy to prove since each metric obeys the %epsilon - %delta criterion. On the other hand the discrete metric

is not topologically equivalent, giving rise to the discrete metric space where each singleton set is open.

In addition, we can define function spaces. Each point in the space is a function, with the metric typically defined in terms of the difference between two functions on an underlying space. The metrics are similar to those above.

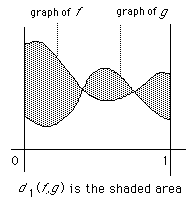
For examplefor bounded functions defined onshown below.

shown below.
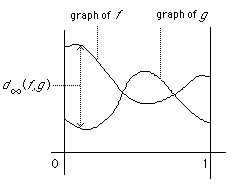