Newton – Cotes formulae use interpolating polynomials to
to evaluate
using leading to the formula
where the
are equally spaced, so
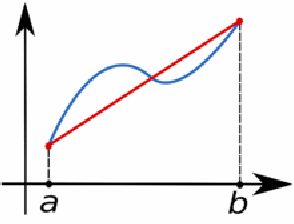
The simplest example of this method is the trapezium rule. It calculates the area of the trapezium formed by approximatingusing linear interpolation. This is shown below for
that interpolates only
and
The trapezium rule can be obtained by integrating the linear interpolation function
over the interval
We can generate other integration rules by using higher order Lagrange polynomials.
The
are labelled
and called weights, thus we obtain
Closed Newton – Cotes formulae include the endpoints
and
in the interpolating polynomial.