An alternative to Lagrange polynomials to interpolate through
points
we can use piecewise polynomial functions called splines, i.e.
where the low degree polynomials
are defined on the intervals
The simplest spline is composed of linear functions of the form
for
(i.e. a straight line between the two successive points
and
).
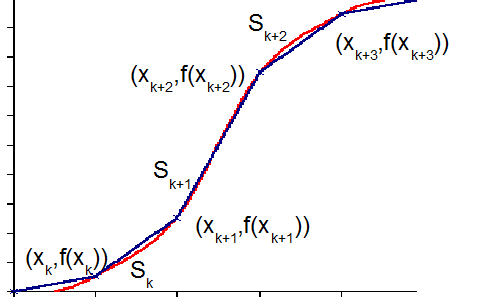
The coefficients
and
are determined by the conditions (i)
and (ii)
Thus,
We need
equations to find thecoefficients
Each of (I) and (ii) gives rise to
equations so
equations in total.
The interpolating function is continuous but it is not differentiable, i.e. not smooth, at the
interior points:
To retain the smoothness of Lagrange interpolation without producing large oscillations, higher
order splines are needed. We can construct splines of any order, but the most common are maybe cubic splines. These are twice differentiable and are suitable for many purposes.