Suppose we have two well ordered sets
and
and a mapping
that maps elements of
to elements of
f is order isomorphic if f is a bijection (one to one and onto) and f satisfies
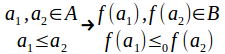
If
is order isomorphic then so is
Well ordered setsandwith the same number of elements are automatically order isomorphic because both sets can be arranged in order and f defined as
The sets of odd natural numbers
and even natural numbers
are order isomorphic, since both sets can be arranged in increasing order and
is a one to one and onto mapping from O to E.
The set of natural numbers
and the set of natural numbers rearranged as
are not order isomorphic since in order forto be onto we must have
somaps
onto the odd natural numbers andis not onto.
We can extended order isomorphisms in the natural way to any number of well ordered sets and order isomorphisms between them.