If a sequence of lifetimes is laid end to end, with then end of each lifetime giving rise to the start of the nex, then we have a Renewal Process. The length of a lifetime can be modelled by any distribution and we are typically interested in the length of
lifetimes.
If the number of renewals in each time period is a Poisson process, with renewals occurring at rate % lambda then the length of each lifetime is the waiting time between renewals. The length of a lifetime obeys an exponential distribution, so that if renewals occur at the rate %lambda then
This means that the time until the nth renewal has a
distribution
We can make the renewal process discrete by considering fixed time units, with the end of an interval of time being givien the time label 1, 2, 3,... Each lifetime is the a positive integer. Many distributions will then return a constant probability of renewal in a time unit. Suppose the probability in each time period is
then the probability of an individual surviving until the nth interval is
for n=1, 2, 3,...
The expected lifetime is then
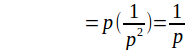
+The expected time to the nth renewal is