The simple random walk describes walking along the x – axis, starting at the origin and randomly moving to left and right, one space at a time.
Definition
A stochastic process
with
is called a simple symmetric random walk if
-
-
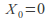
the increment
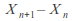is independent of
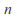and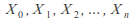
for each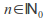
-
the increment
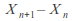has the “coin toss distribution”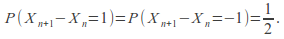
We can define a random variable
to take the continuous uniform distribution on
with 
generating
according to the following rule
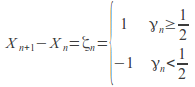
Then setand
Proving this satisfies the requirements of a random symmetric walk is quite easy. 1. is trivially true. To prove 2 note that
is an independent sequence since it is constructed by application of a deterministic function to each element of an independent sequence
then
is independent of all previous
Since the
are linear combinations of the
they must also be independent of
Finally to obtain 3 note that
and similarly for