The Simple Random Walk

The simple random walk is a sequence stating atmoving left or right one step at a time. The probability of moving to the right at any stage isand the probability of moving to the right at any stage is

Definition

A sequenceis called a simple random walk with parameterif

1. 

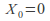
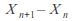2. is independent of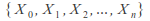for all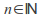

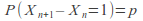3. and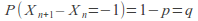

Letbe a simple random walk with parameterThe distribution ofis discrete and takes the valueswith probabilities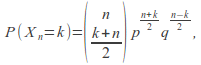(1)

Proof

is composed ofindependent stepseach of which is one to the left or one to the right. In order to reachon the number line insteps the number of steps to the right,minus the number of steps to the left,must be equal toandso thatand(2)

The number of ways in which we can choose thesesteps to the right is then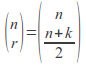(3) and the probability of any individual sequence ofsteps to the right andsteps to the left isSubstitute forandfrom (2) and add all possible sequences of occurrences ofandoccurrences ofto give the factor (3) hence the result (1).