The Ballot Problem

The ballot problem poses the question: If, of two candidates running for office, one wins, what is the probability that the other has led at any stage during the counting process?

More precisely, suppose there are n votes cast in total and the votes are counted one by one. When all the votes are counted, candidate A has won byvotes. Candidate A wo votes and candidate B wonvotes ().

We assume each vote is cast for candidate A with probability(and for candidate B with probability) and the order of counting is independent of the candidate for which the votes are cast. For k ≤ n, letbe the number of votes received by candidate A minus the

number of votes received by candidate B in the firstballots. When thevote is counted,increases by 1 if the vote was for candidate A, or decreases by 1 if the vote was cast for candidate B. The votes are independent of each other andsois (the beginning of) a simple random walk. The probability of increasing by 1 iswhich is not symmetric if

The ballot problem can now be restated as follows:

Find the probability thatfor allgiven?

We must findwhere F denotes the set of trajectories that stay non-negative and G the set of those that reach m at time n. Each trajectory in G has (n + m) over 2 moves right and (n − m) over 2 moves left, so its probability weight is always equal toTherefore,

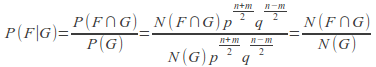
The number of paths inis equal to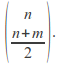We count the number of paths inThe paths inform a portion of all the paths inwhich don’t reach −1, so

thatwhereis the set of all paths which finish atbut cross or touch the level −1 in the process. We can use the reflection principle to findThe reflection of any path in H in −1 after its first hitting time of that level produces a path that starts at 0 and ends atConversely, the same procedure applied to such a path yields a path in The number of paths from 0 tois equal to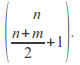Putting everything together, we get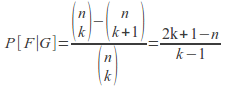where