In the immigration death model individuals join the population according to a Poisson process with parameter
and live a life of length model by an exponential distribution with parameter
Because immigration is constant, there can be no extinction. Similarly the population cannot increase to infinity since if the population is
the number of deaths in any time period
is approximately equal to
and this will exceed the constant level of immigration for x big enough.
The Kolmogorov equations give
for
The population may vary about some equilibrium level. Setting
and letting
represent the equilibrium level of the population being of size
we obtain
and
for
If the number of immigrants is equal to the number of deaths then
or
Hence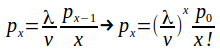
This is a probability distribution so
so that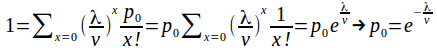
Hence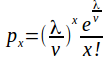
The probability distribution of the population in the long run is a Poisson distribution with parameter