Example of a Uniformly Continuous Function

A functionfrom a metric spaceto a metric spaceis said to be uniformly continuous if, for everythere is somesuch that for every

Suppose now thatand X and Y are both the set of real numbers. Let the metrics onandbe the absolute value topology.

Letthen

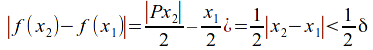so takethenso that