The real valued function![]() is given by
is given by
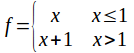
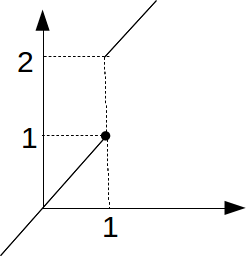
![]() is not continuous if setr is given the ordinary Euclidean topology with metric
is not continuous if setr is given the ordinary Euclidean topology with metric![]() consisting of open intervals of the form
consisting of open intervals of the form![]() but is continuous if
but is continuous if![]() has the upper limit topology . The upper limit topology consists of unions of half open sets of the form
has the upper limit topology . The upper limit topology consists of unions of half open sets of the form![]()
Let![]() be the open set
be the open set![]() in
in![]()
![]() so the inverse image of an open set is not an open set and
so the inverse image of an open set is not an open set and![]() is not continuous with the Euclidean topology.
is not continuous with the Euclidean topology.
The upper limit topology on![]() consists of all half open intervals of the form
consists of all half open intervals of the form![]()
![]()
The inverse image of an open set is an open set nis an open set sof is continuous with this topology.
