Theorem
Every metric space
is normal.
Proof
A topological space is normal if, given any two disjoint closed subsets
and
there are disjoint open sets
and
with
and
Let
be the topology induced on
by the metric
Letandbe disjoint closed sets, then there exists
such that for all
for some
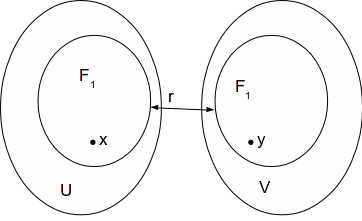
Now take
and
andare disjoint,and
sois normal.