\[f(x)=2x^2-3\]
\[f\]
takes an argument, squares it, multiplies the anser by 2 and subtracts 3.If instead we want
\[f(3x+2)\]
, the function \[f\]
will take \[3x+2\]
, square it, multiply the answer by 2 and subtract 3.A function machine acts in the same way and we can use this to solve problems. Consider the function machines below.
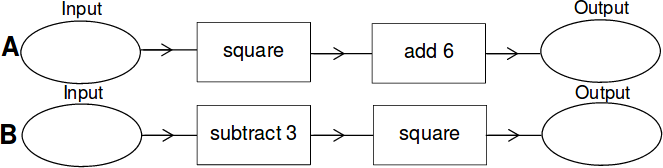
Let the input to each machine be
\[x\]
.The output from A is
\[x^2+6\]
The output from B is
\[(x-3)2\]
Then we require
\[x^2+6 \gt (x-3)^2\]
\[x^2+6 \gt x^2-6x+9 \rightarrow 6x \gt -6x+9 \rightarrow 12x \gt 9 \rightarrow x \gt \frac{9}{12} =\frac{3}{4}\]
. 