Suppose we have a corridor with a corner. End side of the corner has a width of 5m and the other has a width of 3m.
From the diagram
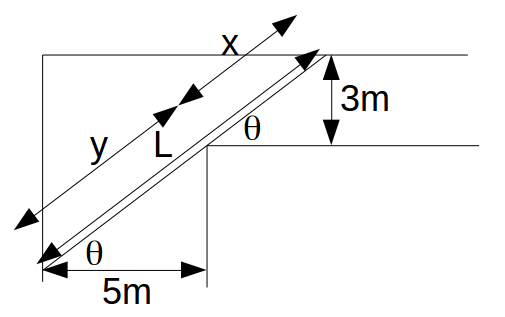
\[L=x+y=\frac{5}{cos \theta}+\frac{3}{sin \theta}\]
Differentiating with respect to
\[\theta\]
and setting equal to zero gives\[\frac{dL}{d \theta} = \frac{d}{d \theta} (\frac{5}{cos \theta}+\frac{3}{sin \theta})=5 sec \theta tan \theta -3 cosec \theta cot \theta =0\]
Hence
\[5 sec \theta tan \theta =3 cosec \theta cot \theta\]
\[5 \frac{sin \theta}{cos^2 \theta} =3 \frac{cos \theta}{ sin^2 \theta}\]
\[\frac{sin^3 \theta}{cos^3 \theta} =\frac{3}{5} \rightarrow tan \theta = \sqrt{3}{\frac{3}{5}}\]
But
\[sec \theta = \sqrt{1+tan^2 \theta}=\sqrt{1+(\frac{3}{5})^{3/2}}\]
and
\[cosec \theta = \sqrt{1+cot^2 \theta}=\sqrt{1+(\frac{5}{3})^{3/2}}\]
Hence
\[L=5 \sqrt{1+(\frac{3}{5})^{3/2}} + 3 \sqrt{1+(\frac{5}{3})^{3/2}}\]
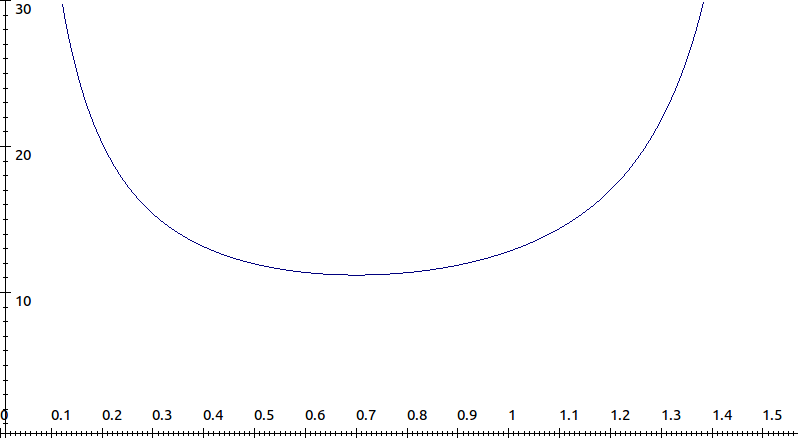
.From the graph the function is obviously a minimum.