Suppose we cut corners of side
\[x\]
from the card.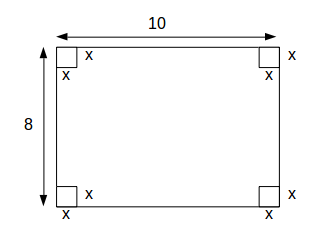
\[x, \: 8-2x, \: 10-2x\]
.The volume is
\[V=x(8-2x)(10-2x)=4x^3-36x^2+80x\]
.To find the maximum volume, start by differentiating.
\[\frac{dV}{dx}=12x^2-72x+80\]
Solve the equation
\[\frac{dV}{dx}=0 \rightarrow 12x^2-72x+80=0 \rightarrow x=\frac{9 \pm \sqrt{21}}{3}\]
.Now differentiate again to find
\[\frac{d^2V}{dx^2}\]
and substitute these values of \[x\]
. If the result is greater than zero, the result is a local minimum for the volume, and if the result is less than zero, the result is a local maximum for the volume.\[\frac{d^2V}{dx^2}=24x-72\]
\[x_1=\frac{9 - \sqrt{21}}{3} \rightarrow \frac{d^2V}{dx^2}=24x_1-72=24(\frac{9 - \sqrt{21}}{3})-72=-8 \sqrt{21} \lt 0 \]
so this returns a maximum volume.\[x_2=\frac{9 + \sqrt{21}}{3} \rightarrow \frac{d^2V}{dx^2}=24x_2-72=24(\frac{9 + \sqrt{21}}{3})-72=8 \sqrt{21} \lt 0 \]
so this returns a minimum volume.The maximum volume is
\[V(x_1)=4(\frac{9 - \sqrt{21}}{3})^3-36(\frac{9 - \sqrt{21}}{3})^2+80(\frac{9 - \sqrt{21}}{3})=\frac{216+56 \sqrt{21}}{9}=52.5 \: units^3\]
