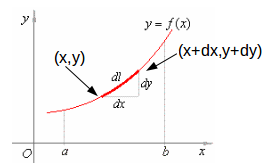
\[(x,y), \: (x+dx, y+dy)\]
is from Pythagoras theorem, \[dl=\sqrt{(dx)^2+(dy)^2}=\sqrt{1+(\frac{dy}{dx})^2}dx\]
.The length of the curve from
\[x=a\]
to \[x=b\]
is then just the integral of this.\[L=\int^b_a \sqrt{1+(\frac{dy}{dx})^2}dx\]
.