Finding the Equation of a Polynomial Given Two Purely Imaginary and One Real Root

If a cubic polynomialwhereis real, has a real root and two purely complex roots, we can find the value ofand the complex roots by deriving simultaneous equations.

Since the coefficients of the polynomial are real, the purely complex rootsand occur as a complex conjugate pair so that we can writeandIf the real root isthe the polynomial can be written as

Then from considering the coefficients of

(1)

(2)

and the constant term gives(3)

(3) divided by (2) gives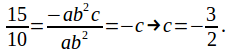

Then from (1)

Then from (2),

Then