Finding the Equation of a Quartic

The equation of a quartic can have up to five constants:

This means we need five conditions to determine the equation of the quartic. In fact we always need five condtions, but some of these may be hidden. If the equation of the quartic includes a repeated factorthen the corresponding condition would be ' the graph of the quartic is a tangent at'. This statement includes two conditions.

1. is a tangent

2. at

Taking this sort of thing into account, we can find the equation of the quartic.

Example: Find the quartic which touches the x - axis at 3, cuts it at -2 and also passes

throughand

1. ' touches the x - axis at 3' implies the quartic is a tangent atso includes a factor

2. ' cuts it at -2' implies a factor

The quartic must then take the form

passes throughso (1)

passes throughso (2)

(1) divided by (2) gives

Then from (2)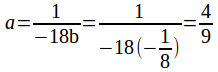

The equation of the quartic is