Exponential equations contain terms such as 3x or e3x . To solve the equation we find x. There may be no solution for x, one solution or more than one. Often we may substitute for x to simplify, solve the simplified equation then use the substitution to find x. If the equation is simple, we only need to make x the subject or solve by inspection.
Example: Solve
By writing
we have
by identifying powers. It is easily seen now that
Example: Solve
Since the base is the same on both sides (it is equal to 3), we can equate the powers to give
If the bases are not the same but are related, we may be able to make them the same.
Example: Solve
We can use one of the indices laws to write
then the equation becomes
The base is the same on both sides so we can equate the bases, obtaining
This can easily be solved:
If the bases are not related, we can still solve the equation, but we must take logs.
Example: Solve
Taking logs gives
Expand the brackets and collect coefficients of
Now divide by
the coefficient of
to give
This can be evaluated by calculator, but this does not give an exact answer. We can instead make a single log of numerator and denominator, obtaining.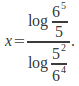
Example: Solve
This has no solutions. We can raise a real number to a negative power, but the result, if the power is real, can never be a negative number.
Example: Solve
Substitute
then
and we obtain
We can factorise this to obtain
then
or
Use the substitution now to obtain
or